How to avoid the “beat” and request “flooding” of the system

The solution to this problem came to me during my work on the game called Soldiers: Heroes of World War II. I developed a movement system for tanks and other vehicles for this game.

From time to time tanks would block each other or get stuck on obstacles when moving in groups. In this case, the player could manually drive it around the obstacle or cancel the order. Sometimes the tanks would overcome these obstacles on their own, and the player would not have to repeat orders. However, the player still had to babysit his tanks so that they would not get stuck .

To fix this, I  made the orders repeat automatically after a constant delay. At first glance, it seemed like a logical decision. But it led to the problem where all the stuck tanks were trying to drive around an obstacle at the same time. It led to a surge in the load on the pathfinding subsystem and a noticeable stutter in the game. There was a so-called beating effect.

There was also the effect of a simultaneous resolution of conflicts – both tanks clashed when trying to overtake each other at the same time. It is like if two people on a narrow sidewalk tried to give each other a way while sidestepping in the same direction.

When my first solution failed, I tried to execute the order repetition using a random interval in a given time range. I managed to eliminate the “beating” and “endless cycles” that occurred while attempting to resolve conflicts.

But there was a problem with this elegant solution. The more time passes, then fewer are the chances that the situation has gotten any better since last time. So there was no point in overloading the system with constant checks.

The third solution was born by multiplying the wait time by a fixed amount after each attempt. After a certain number of attempts, it makes sense to stop the pointless waiting or to limit the time between checks, as it will go beyond the limits of reasonable values.

The result is a restart algorithm for failed operations, which looks like this:

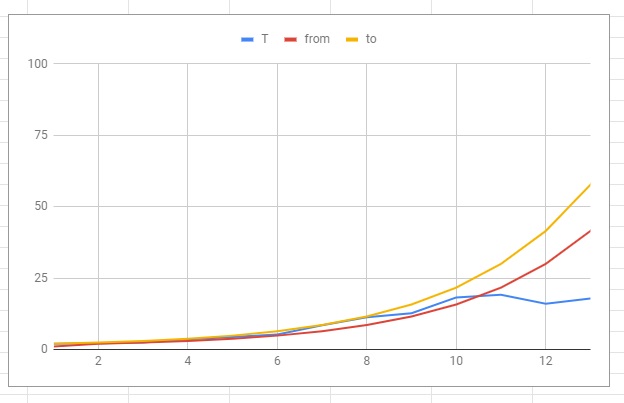
Parameters:

1. T₀ – minimum wait time
2. C_high  – the number of attempts below which the waiting time increases
   • 1 < C_high <= C_max
3. C_max – the maximum number of attempts
   • C_max >= 1
4. D – the maximum random spread of time at the first attempt
   • must be > 0
5. S – coefficient of the increasing waiting time at each subsequent step
   • must be > 1

Algorithm:

1. set the attempt counter C ← 0
2. perform the operation
3. if the operation is successful, then
   • we leave with success
4. C ← C + 1
5. if C >= С_max, then
   • exit with error
6. if C = 1, then
   • waiting time T ← T_min + D * (random variable from 0 to 1)
7. otherwise
   • X ← min(C_high, C) – 2
   • waiting time T ← T_min +  D * (S^X + (random variable from 0 to 1) * (S^X+1 – S^X)
8. wait for time T
9. go to point 2

This algorithm can be used in any automatic failure recovery processes. For example:

• to determine a reasonable time to reconnect the client to the server;
• in computer games so that the AI ​​does not look like a dummy;
• collision resolution in network;
• restarting programs after crash;

The same algorithm was used later in the development of InvariMatch to restart failed operations. It allowed us to ensure system stability, avoid server overloading due to the repetition of failed requests and to add automatic system recovery after local and global crashes.